Yabu.log

ITなどの雑記

手ぶら通勤を一週間やってみた

ライフハック

手ぶら通勤を１週間やって見たみたので、その記録でも書きます。 rebuild fmに出てるhigeponさんの影響です。*1

持ち物

  • カバンを持たない
  • 財布、携帯、メモ、文庫本のみ。
    • メモはJET ACEという背表紙に挿せるミニ鉛筆が付属するものを使ってる
    • 本当はすぐログという手帳が欲しかったが、同メーカーの類似品でこっちの方が安かったのでけち臭くコレをチョイス
    • メモの出番はあまりなかった。

ダイゴー メモ すぐログ 鉛筆付き 手帳 ターコイズ A1291

ダイゴー メモ すぐログ 鉛筆付き 手帳 ターコイズ A1291

ダイゴー ノート ジェットエース クロ A1155

ダイゴー ノート ジェットエース クロ A1155

メリット

  • 満員電車でもそうでなくても非常に快適。
  • 肩に感じる重さがなくなることがここまで快適だとは思わなかった。

デメリット

  • 雨が降ると傘を持参する必要が出てくるので完全に手ぶらとはいかなくなる。
  • 忘れ物が不安
  • 私物PCは会社に置きっぱなしなので、雪のときに在宅勤務に切り替えるなどの柔軟な働き方ができなくなる。
  • 電車の中で技術書を読む時間が減る。
    • 持ち歩く読み物としては文庫本を持ち歩いている。
  • 会社以外でやってる勉強会に出るときは流石に荷物が要りそう。

発展

suicaもスマホのものを使えるし、この際財布もいらない気がしてきた。

総評

というわけで、カバンが必要ないなら持っていかないに越したことはありませんが、 カバン有り無しの切り替えを考えるのが結構面倒です。 少なくとも私は重要なもの(印鑑や入館書など)を特に意識せずカバンに突っ込んだまま会社と自宅を往復してきました。 カバンを持たないというのはその怠惰に向き合うことになります。

...と大層な書き方をしていますが、他の人と雑談したところ、手ぶら通勤ON/OFFの切り替え時に忘れ物が増えるのはあるあるのようです。 今後も運用するかは微妙。

*1:https://rebuild.fm/228/

Transaction,Concurrency ControlとAntichain

order theory computer science

グラフのトポロジカルソート可/不可のみでアノマリーの検査やSerializabilityの判断をするのではなく、Order Theoryの知見をConcurrency Conntrolに活用しようという動きがあるらしい。そしてantichainというorder theoryの概念がわからなかったのでそのメモ。

本エントリはほぼwikipedia:enのantichainの翻訳です。(2019/10/25時点不完全)

en.wikipedia.org

Antichain

Order theory におけるAntichainとは半順序集合の元の内、二項関係が比較不能になる元のみを集めた部分集合のことである。

半順序集合 S中の要素a,bの間に成り立つ性質を以下のように定義する

  • comparable
    • a ≤ bかb ≤ aが成り立つ
  • incomparable
    • a ≤ bとb ≤ aの両方が成り立たない

comparable,incomparableの概念を導入することで半順序集合は二つの部分集合に分割することができる

  • comparableな元のみで構成される部分集合をChainと呼ぶ。
  • incomparable元のみで構成される部分集合をAntichainと呼ぶ

Height and width

f:id:yuyubu:20191025212239j:plain
二分木を例にしたchain,antichainとheight,widthのイメージ

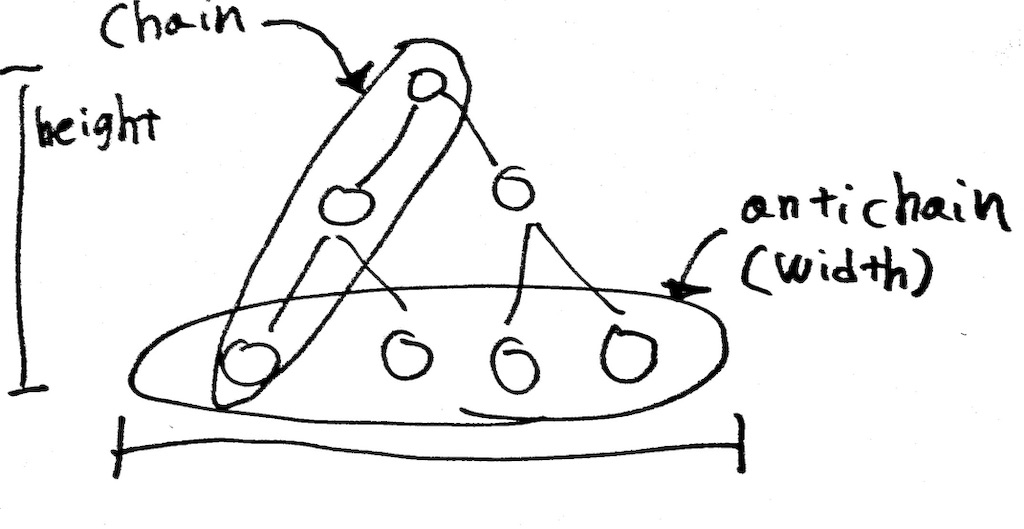
  • maximal antichain:他のantichainの部分集合にならないようなantichain
  • maximum antichain:poset*1の中でもっとも多くの元を含むantichain
  • width:posetのmaximum antichainの濃度のこと
    • posetがk個のchainに分割できる場合、antichainのwidthはk以下になります。

  • height:posetのchainのもつ、最大の濃度のこと

    • hightとantichainの最小個数は一致する*2*3

  • 任意のantichainがchain共通部分を持つ場合、共通部分の濃度は高々1つです。

    • antichainにはcomparableな元を含めないため,あるchain(任意の元のペアがcomparableな性質をもつ)の元が複数入っていることはおかしい

Sperner families

  • あんまり関係なさそうなわりにハイコンテキストなので訳さない。原文↓

An antichain in the inclusion ordering of subsets of an n-element set is known as a Sperner family. The number of different Sperner families is counted by the Dedekind numbers, the first few of which numbers are

Join and meet operations

  • note:ここから下はあまり自信がありません...

  • おそらくorder theoryにおけるJoin,meetと言う概念の理解が必要と思われる。

  • 全てのantichainには対応する下方集合(lower set)が存在している。

  • ちなみに,Xの部分集合である下方集合Lは次のように定義できます*4

∀x∈L ∀y∈X: y≤x ⇨ y∈L

  • note:これはposetをグラフ化したとき、antichainとなる集合には必ずin-degreeが1以上にの元がある、ということかな。(antichainから開始するグラフは作れない=必ず下方集合が存在する)

  • 対応する下方集合の違うantichain A,Bに対して以下の条件JOIN∨操作を行うことができる。

    • A∨B = {x ∈ A ∪ B | !∃ y ∈ A ∪ B s.t.x<y}

  • 似たようにmeet∧操作を行うことができる

    • A∧B={x∈LA∩L|!∃y∈LA∩LB s.t. x < y}

*1:partial order setの略称。一般的なので本エントリでも使う

*2:これよくわからない

*3:Mirsky's theorem states similarly that in any partial order of finite height, the height equals the smallest number of antichains into which the order may be partitioned.

*4:https://en.wikipedia.org/wiki/Upper_set

Amazonにレビューの掲載を拒否されました

Amazon

たまたま購入した商品のマーケットプレイスで偽物を出品している業者があとを絶たず、ページ内でメーカーが警告を書いているような異常な状態に出くわしました。

購入後に役立つ情報だろうと思い以下のようなレビューを投稿しました。*1

  • レビュー内容
    • 偽物が多く出回っているので正規品のパッケージを載せるので参考にして欲しい。という趣旨の文章
    • 商品のパッケージ画像を数枚掲載

数日後、レビュー掲載を拒否するという旨のメールがアマゾンからきました。

お客様レビューを送信していただきありがとうございます。

Amazonのお客様レビューを送信していただきありがとうございます。 お寄せいただきました送信内容を慎重に確認した結果、お客様のレビューをウェブサイトで公開することはできませんでした。 お時間を取ってコメントしていただき感謝いたしますが、レビューは次のガイドラインに従っている必要があります。 http://www.amazon.co.jp/review-guidelines

主な注意事項は以下の通りです:

・レビューを書く際は、その商品特有の機能とその商品を実際に使用したあとの感想を中心に書き込んでください。出品者や配達に関するフィードバックは、www.amazon.co.jp/feedback でご提出ください。
・次のようなレビューは禁止されています：不敬またはわいせつな内容（アダルト製品を含むすべての製品について）、金品などの対価を受けることを目的とした内容、薬事法等の適用法令に抵触する内容
・広告、宣伝資料、または同じ要点を過度に繰り返す投稿はスパムと見なされます。
・レビューには、Amazon 外の URL または個人的にしか特定できないコンテンツを含めないでください
・コミュニティのコンテンツや機能を操作しようとする試みは固く禁じられています。これには、誤った内容、誤解を招くおそれがある内容、正しくない内容の送信が含まれます。

不満とか怒りとかは特にないのですが、きちんとチェックしていることにちょっと驚きました。 確かに自分が投稿した内容は直接商品を評価する内容でないのは事実です。 意外とレビュー内容を人間かかなりよく訓練されたAI的なもので精査しているのでしょうか。

中華系業者による少しおかしな日本語レビューも弾けよ、と思いましたが、サクラという点では排除すべきですが、 レビュー内容は日本語が片言の外国人が一生懸命書いたレビューとなんら変わりないもののはずですし、ガイドラインには違反しないように書かれているのでしょう。

ちょっと意外だなと思ったことなのでブログにしてみました。みなさんもレビューするときはガイドラインに抵触しないように気をつけましょう。

*1:余談ですが、海外では商品が偽物でないことの確認のためにyoutubeの開封動画を参考にするという話を聞いたことがあります。

Chrome拡張を使ってAmazonの検索ページから怪しい中華業者を一掃する方法

ライフハック Amazon

正規表現でアクセスするURLを変える拡張機能を使って、以下のページで紹介されているパラメータをURL末尾につけるように置換するだけです。

n-styles.com

  • Redirector

chrome.google.com

  • 設定内容

From

(https://www.amazon.co.jp/s\?.*)

To

$1&emi=AN1VRQENFRJN5

f:id:yuyubu:20200903123036p:plain
設定内容はこんな感じ

f:id:yuyubu:20191022014157p:plain
before

f:id:yuyubu:20191022014315p:plain
after

なぜかスポンサープロダクトも消えるという謎副作用が？？？？ 今までパラメータをググって自分でURL末尾にポチポチ付け足してましたが、これで検索ボタン押した瞬間にパラメータが有効になるので楽。 自分はChromeではログインせずにブラウズしかしませんが、これでそこそこ使えそうです。

※多分怪しい中華業者以外も色々消えちゃってると思いますが。

2020/09/03追記:Fromの誤りを修正。DocSeriさんありがとうございます

Hadoopの勉強をはじめました。

Hadoop Distributed System

Hadoopはレイテンシを犠牲にIOを分散させて高速なバッチ処理を実現する技術、という程度のことしか知りません。*1

今在籍している会社分散処理やメニーコアコンピューティング、Spark,Hadoopなどをコアにやってて、エンタープライズ用のHadoop関係のFrameworkを開発・保守したり、そのSIをやっています。

ユーザーとしてFrameworkを使っている分には特にHadoopの知識は特に必要ない*2*3のですが、自分の関わってる案件でもHDFSとかの生のHadoop要素が使われ始めてきたので危機感を持って勉強し始めました。

主に勉強した内容はサブブログに連載する予定です。

yuyubu-sub.hateblo.jp

*1:この理解が正しいかどうかは不明

*2:知っとけやという話もある

*3:というかFrameworkの目的がHadoopわからないJavaエンジニアでも簡単にシステムを保守できるというものであるように思っている

論理学をつくる練習問題80(2)解答

論理学

本に回答が乗っておらず、ネットに載せておく意義があると思ったので公開。 練習問題80(2)はND公理系(自然演繹)で式集合が矛盾するか、どうかの解答と矛盾していればそれを証明(自然演繹で示す)をする問題。 (a),(b),(c)とあるが式集合は全て矛盾しているためその証明(自然演繹による⊥の導出)のみを示す。

※間違ってたらすいません

論理学をつくる

論理学をつくる

問題

Γ⊢NDA, Γ⊢ND¬Aなる論理式Aがあるとき、ΓをND矛盾しているということにする。次の うちND矛盾している論理式の集合はどれか、そしてそれがND矛盾していることを示せ。

  • (a) {P∨Q, ¬P→Q, ¬P}
  • (b) {P∨Q, ¬(P∧Q), P↔︎Q}
  • (c) {P→Q, P, ¬Q}

回答

(a)

P∨Q      Prem
¬P→¬Q    Prem
¬P        Prem
--------------
¬P→¬Q    Rep
¬P        Rep
¬Q        → elim

    Q    Prem
    ---------
    ¬Q    Reit
    ⊥    ¬intro*

Q→⊥    →intro

    P    Prem
    ---------
    ¬P   reit
    ⊥   ¬intoro*

P→⊥   →intro
Q→⊥   Rep
P∨Q    Rep
⊥      ∨elim

ポイント:演繹三行目で∧intoroをつかって¬P∧¬Qを導けるが、これが前提のP∨Qと矛盾していることは明らか(真理値表を書けば真になる割当が見つからない)。またド・モルガンの法則により¬P∧¬Q = ¬(P∨Q))だが、自然演繹に¬P∧¬Q,P∨Qから⊥を導くルールがなく、自然演繹の中のルールで他の式から⊥を導く必要がある。

(b)

P∨Q       Prem
¬(P∧Q)    Prem
P↔Q       Prem
---------------
    P    Prem
    ---------
    P↔Q    Reit
    Q       ↔elim
    P∧Q    ∧intro

P→(P∧Q)    →intro
     
    Q    Prem
    ---------
    P↔Q    reit
    P       ↔elim
    Q       Rep
    P∧Q    ∧intro

Q→(P∧Q)    →intro
P→(P∧Q)    Rep
P∨Q         Rep
P∧Q         ∨elim
¬(P∧Q)      rep
⊥           ¬intoro*

(c)

一番簡単と解答に書いてあったやつ。これを(a)にして最初に解かせてほしかったな。

P→Q
P
¬Q    Prem ⊥
--------------
P→Q    Rep
P       Rep
Q       →elim
¬Q      Rep
⊥      ¬intor*

なにかあればコメントください。

ちなみに、論理学をつくるはまだ挫折しておらず、ノートをサブブログの方に書き出しています。Twitterやめた僕が悪いんだけど、アクセス数3とかなので悲しい(涙)

yuyubu-sub.hateblo.jp

フィッチスタイルの自然演繹のやり方

論理学

完全に個人のメモ。復習+忘れた時に思い出す用。範囲としては論理学をつくるp214~p235。気が向いたら述語を自然演繹で導出対象にするやり方も書くかも。

論理学をつくる

論理学をつくる

式集合の充足可能性の検査には真理表、タブロー、などの複数のやり方があり、自然演繹もそれの一種。

導出線と前提棒

(1) P → Q (前提)
(2) Q → R (前提)
(3) R → S (仮定)
(4) P      (仮定)
(5) Q      (4)と(1)より {P → Q, P}
(6) R      (2)と(5)より {Q → R, Q}
(7) S      (3)と(6)より {R → S, R}
(8) P → S (4)と(7)より {P⊨S}
(9) (R → S) → (P → S) (3)と(8)より

上記だとどの式がどの前提に依存しているのかわかりにくい。 仮定が生きてるスコープを表すために、導出線、仮定の宣言に前提棒というシンタックスを導入する

  • パソコンでノートを作る都合上、導出線をインデントで表す。
  • 前提棒を式下の---------で表す。
(1) P → Q (前提)
(2) Q → R (前提)
-----------
    (3) R → S (仮定)
    -----------
        (4) P      (仮定)
        ------
        (5) Q      (4)と(1)より {P → Q, P}
        (6) R      (2)と(5)より {Q → R, Q}
        (7) S      (3)と(6)より {R → S, R}
    (8) P → S (4)と(7)より {P⊨S}
(9) (R → S) → (P → S) (3)と(8)より
  • 導出棒上の演繹は自分が書かれた導出棒より浅い(左)に存在する前提を参照することはできない。

演繹規則

表記

  • 適応した演繹規則を導出した論理式の右側にやや空白をあけて表記する
    • 本ブログではスペース4個とする
  • みやすさの観点から、同じ階層の導出ではこの規則表記を一番長い論理式のスペースに合わせる
例

P       Prem
P→Q    Prem
Q       →elim

前提規則(premiss rule:Prem)

  • (1)導出開始時の最初の前提棒状に書ける論理式の個数に制限はない。 例:(i)
  • (2)それ以外の前提棒の上には一つしか論理式をかけない。 例:(ii)

(i)

P → q Prem
¬Q∧R   Prem
S→¬P  Prem
------

(ii)

P → q Prem
¬Q∧R   Prem
S→¬P  Prem
-----------
    P  Prem
    -------

繰り返し規則(rule of repetition: Rep)

  • その導出の前提棒の上にある式を繰り返し書いて良い。
    P    Prem
    ---------
    P    Rep
P → P    → intro

復活規則(rule of reiteration:Reit)

  • 依存している導出(有効なスコープである前提)を繰り返し書いても良い。

例

(P → Q) ∧ ¬Q    Prem
---------------------
P → Q    ∧ elim
¬Q        ∧ elim
    P         Prem
    ---------
    P → Q    Reit
    Q         → elim
    ¬Q        Reit

→除去規則(→ elimination: → elim)

  • A → B と A が同じ導出に出てきたら、Bをその導出中に書き加えて良い
P →Q    Prem
P        Prem
---------
P →Q    Rep
P        Rep
Q        → elim

→導入規則(→ introduction: → intro)

  • 前提AからBへの導出を含んでいるならば、A→Bをその導出後の項目に書き加えて良い。
P→Q    prem
Q→R    prem
    P         prem
    ----
    P → Q    reit
    Q         → elim
    Q→R      reit
    R         →elim
P → R    → intro

∧除去規則(∧ elimination: ∧ elim)

  • A ∧ Bが導出の一項目として現れているなら、A,Bいずれもその同じ導入の項目として書き足して良い。
A ∧ B    Prem
A        ∧ elim

あるいは

A ∧ B    Prem
B        ∧ elim

∧導入規則(∧ introduction:∧ intro)

  • AとBがいずれも同じ導出の項目として現れているなら、A∧Bをその導出の一項目として書き足して良い。　
A
B
A ∧ B    ∧ intro

↔︎除去規則(↔︎ elimination:↔︎ elim)

  • A ↔ ︎BとA(あるいはB)が導出に一項目として現れていたら、その導出にもう片方のB(あるいはA)を書き加えて良い。
A ↔︎ B
A
B        ↔︎ elim

↔︎導入規則(↔︎ introduction:↔︎ intro)

  • A → BとB → Aが一つの導出に一項目として現れてきていたら、その導出にA ↔ ︎︎︎Bを書き加えて良い。
A → B
B → A
A ↔︎ B    ↔︎ intro

¬削除規則(¬ elimination: ¬ elim)

  • ¬¬Aの導出に¬Aを書き加えて良い
¬¬A

A    ¬ elim

¬導入規則(¬ introduction:¬ intro)

  • Aを仮定とした導出から矛盾(contradiction)が発生した場合、導出の次の項目に¬Aを加えて良い
    A    prem
    ---------
    ...
    B
    ...
    ¬B    contradiction !
¬A    ¬ intro

∨除去規則(∨ elimination:∨ elim)

  • A ∨ B,A→C,B→Cが導出に出てきた場合、Cを書き加えて良い
A ∨ B
A→C
B→C
C      ∨ elim

∨導入規則(∨ introduction:∨ intro)

  • AかBが同じ導出において以前に一項目として出てきているなら、A ∨ Bを書き加えて良い
A
A ∨ B    ∨ intro
B
A ∨ B    ∨ intro

矛盾記号(⊥)の導入

  • contradiction!を論理定項として使うとほかの∨ elimや→ introなどのオペランドとして使えるのでより演繹の自由度が上がる。
  • 矛盾記号⊥を導入する。

¬elim*

  • 矛盾する式集合(A,¬A)が導出に現れた場合、⊥をその導出に書き加えて良い
A
¬A

⊥
  • ※矛盾記号の¬elim*を導入する場合、これまでの¬elimの規則はDNという名前に変更する

¬intro*

    A
    --
    ⊥
¬A

自然演繹の攻略法

【攻略法:→を目指すには】

  • A → Bに達したい時,Aを前提とし、一番下にBが出てくるような導出を構成し、→ introによってA → Bを得るようにする

【攻略法:∧を目指すには】

  • A ∧ Bに至りたかったら、AとBをそれぞれ別個に得るようにし、そのあとに∧ introを用いると良い。

【攻略法:間接証明】

  • ¬Aを仮定して矛盾を起こして¬¬Aを導出し、¬elimでAを得ることができる。
    • 個人的に背理法のような戦略だと思う