多分Polygraphについて書かれた2番目の日本語のエントリー。*1
日本初のエントリー↓
内容としては先行している記事が複数の文献を参照していますが、このエントリはTheory of Database Concurrency Control p35~37の要約になっています。
polygraphとは
- VSRのvalidationを行う特殊なグラフ
- 定義:Polygraph P=(V,A,C)
- V:vertex 頂点の集合
- A:arc (
V * V) - C:choice (
V * V * V)

compatible
- P=(V,A,C)と次の関係がある有向グラフD(V,B)をPとcompatibleという
- A ⊂ B
- 全てのchoice (u,v,w )⊂C ,(u,v)∈B または (v,w)∈B
- 具体例次のPolygraph P1はD1,D2とcompatible
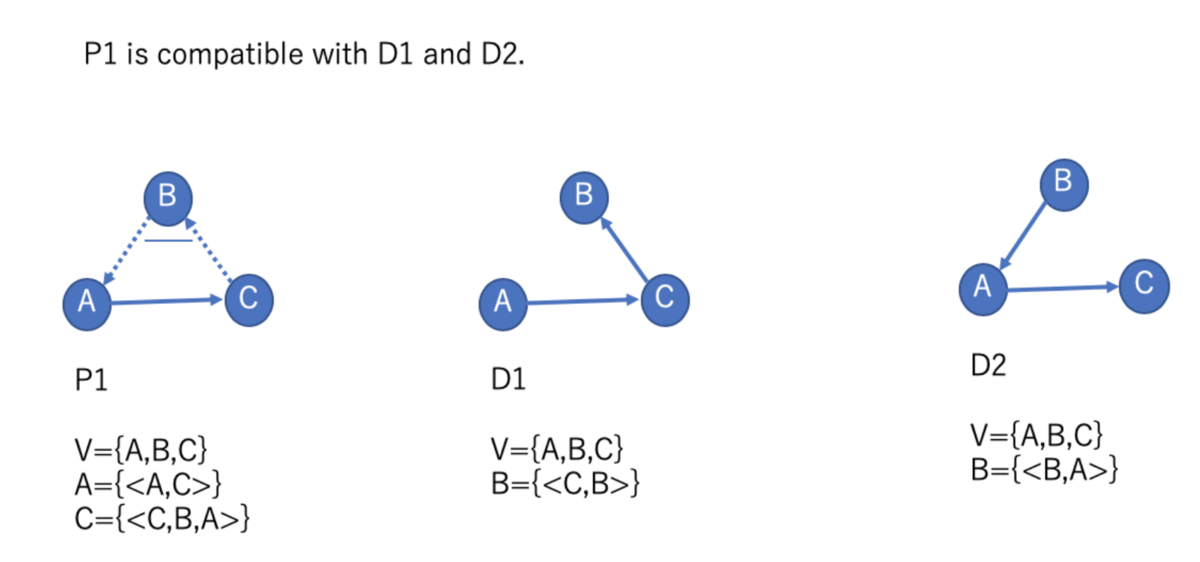
- もう少し複雑な例

acyclic Pollygraph
次の性質を持つPolygraphをacyclicであるという
- Polygraph PにcompatibleなDAGが存在する
Plygraphとcompatibleなグラフの中でacyclicなものが存在すれば、polygraphはacyclicであるという
スケジュールをPolygraphに変換する方法
複数のトランザクションの集合をscheduleとする
- schedule sの全てのトランザクションの先頭に
と末尾に
を含めた
をVertices Vとする
Arcの作成:
に存在する全てのトランザクションA中のRに対して以下の操作を行う
∈
の以前に存在している直近のWrite
∈
からArc(
,
)を作成しPolygraph PのArc Aに追加する
- 備考:通常、s中の全てのentity xに対してW(x)が
に存在しているため、
にはWriteに後続しないReadは存在しない=arcはs中のRの数存在している
- 備考:通常、s中の全てのentity xに対してW(x)が
choiceの作成:arcを作成する際に使った
<
に対してs中に
以外のトランザクション
に
が存在する場合、choice(
)を作成しPolygraph PのCに追加する
- ※
は
ではなく、sの要素であることに注意。(
はchoiceの中間ノードとして選択できない)
- ※
スケジュールsから作成したPolygraphをP(s)と表記する
P(s)とcompatibleに必要なもう一つの制約
P(s)とcompatibleなdigraph D=(V,B)はA0を支点とし、A∞を終点とするようなグラフではないといけない*2。つまり、以下に再掲するcompatileの条件にA0,A∞に関する制限が追加される。
全てのchoice (u,v,w )⊂C ,(u,v)∈B または (v,w)∈B
- P(s)のCに
を含んでいるchoice(
)があるとき、Bは(
)を含んではならない
- P(s)のCに
を含んでいるchoice(
)があるとき、Bは(
)を含んではならない
- この制約がないと、前者は
に先行するトランザクションが、後者は
に後続するトランザクションが存在してしまっているようなおかしなscheduleが出来上がってしまう。
ScheduleからPolygraphを作成する具体例
- 以下のスケジュールからPolygraphを作成する
s=r1(x)w2(y)w1(y)r3(x)w2(x) A1: R(x) W(y) A2: W(y) W(x) A3: R(y)
- Vertex Vはs中のA1,A2,A3に
を加えた
V={A0,A1,A2,A3,A∞}
- Arc Aは
中の四つのreadと同一entityに対する直近のwriteから構成される
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
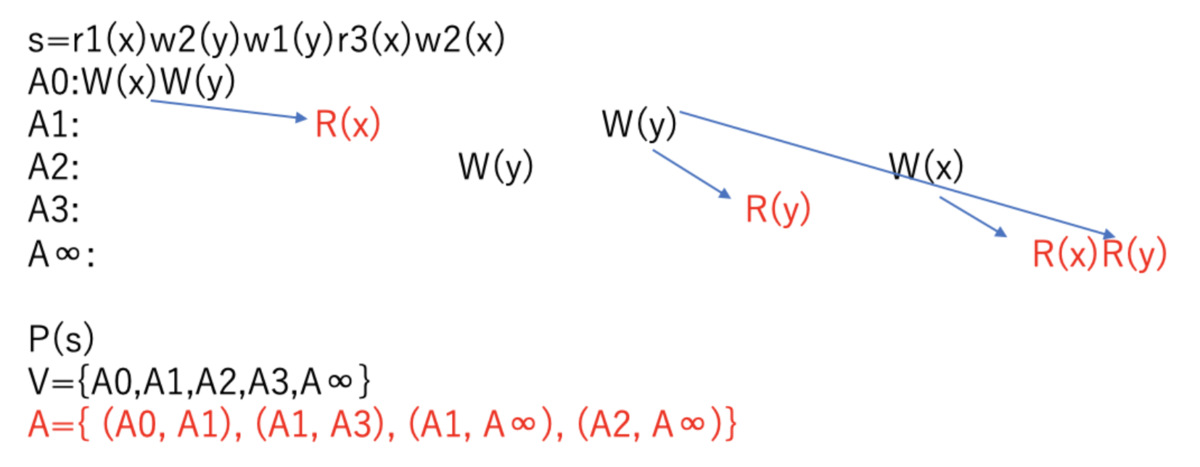
- choiceは各Arcを作っているstepと同一entityに対してs中の他のトランザクションがwriteを行なっているかを検査することで求めることができる
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}- (A0,A1):xにより作られたArc→A2がW(x)を含んでいる→choice(A1,A2,A0)
- (A1,A3):yにより作られたArc→A2がW(y)を含んでいる→choice(A3,A2,A1)
- (A1,A∞):yにより作られたArc→A2がW(y)を含んでいる→choice(A∞,A2,A1)
- (A2,A∞):xにより作られたArc→他のA∈sがW(x)を含んでいないためchoiceの追加はなし。
- A0がW(x)しているのでは?と思われたかもしれませんが、定義を再確認し、choiceの中間ノードにA0,A∞は入らないことに注意してください
ビジュアライズ
必要な要素が出揃ったのでP(s)をビジュアライズする破線がchoiceのedge,実践がarcのedgeです。
s=r1(x)w2(y)w1(y)r3(x)w2(x)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}
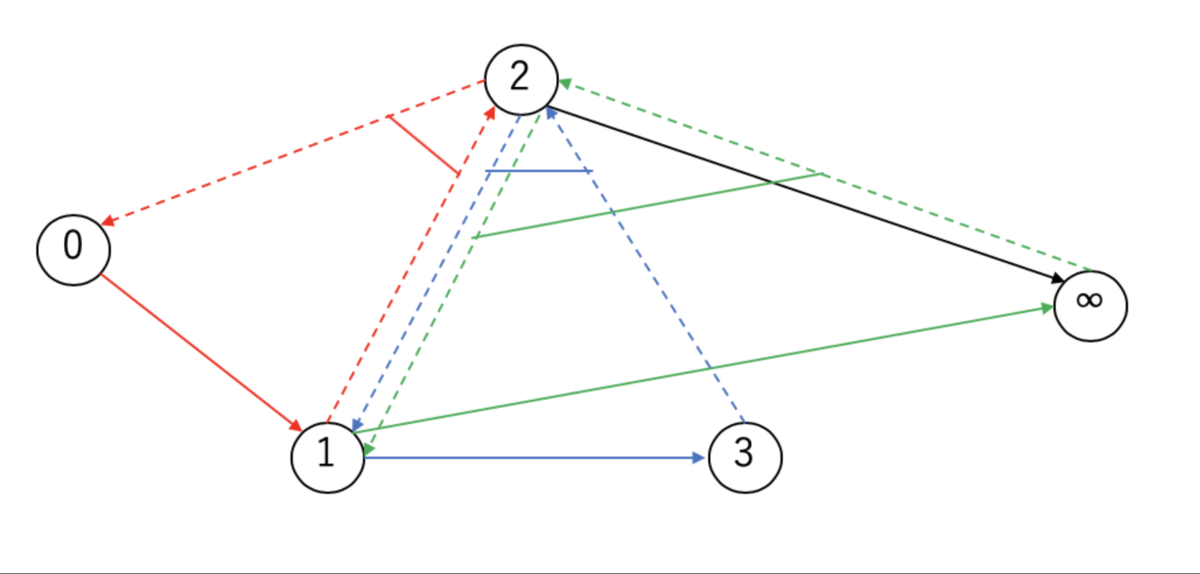
このP(s)はChoice (A1, A2, A0), (A∞, A2, A1)を含んでいる。A0,A∞とchoiceに関するルールにより、P(s)とCompatibleなdigraph(V,B)は必ずBに(A1,A2)と(A2,A1)を含んでいる。
- A0,A∞とchoiceに関するルール再掲
- P(s)のCに
を含んでいるchoice(
)があるとき、Bは(
)を含んではならない
- P(s)のCに
を含んでいるchoice(
)があるとき、Bは(
)を含んではならない
- P(s)のCに
これにcompatibleなdigraphは(A1,A2)間で発生するcycleを持つためacyclicではない→P(s)はacyclicではない。
計算クラス
VSRの検査はNP完全です
詳しくはデヴすぴスラさんのブログを読んでください。概略だけ箇条書きしておきます
- VSRのvalidationがNP完全
他
かなり難しい.実際は[エルブランセマンティクス(Herbrand Semantics)]と[Reads-From]で[VSR]を,[Multiversion Serialization Graph(MVSG)]で[MVSR]を定式化できるので,覚えなくてもいい.
だそうです。うーんすごく時間を無駄にした気分だ。

Theory of Database Concurrency Control
- 作者:Christos Papadimitriou
- 出版社/メーカー: Computer Science Pr
- 発売日: 1986/07/01
- メディア: ハードカバー