グラフのトポロジカルソート可/不可のみでアノマリーの検査やSerializabilityの判断をするのではなく、Order Theoryの知見をConcurrency Conntrolに活用しようという動きがあるらしい。そしてantichainというorder theoryの概念がわからなかったのでそのメモ。
本エントリはほぼwikipedia:enのantichainの翻訳です。(2019/10/25時点不完全)
Antichain
Order theory におけるAntichainとは半順序集合の元の内、二項関係が比較不能になる元のみを集めた部分集合のことである。
半順序集合 S中の要素a,bの間に成り立つ性質を以下のように定義する
- comparable
a ≤ bかb ≤ aが成り立つ
- incomparable
a ≤ bとb ≤ aの両方が成り立たない
comparable,incomparableの概念を導入することで半順序集合は二つの部分集合に分割することができる
- comparableな元のみで構成される部分集合をChainと呼ぶ。
- incomparable元のみで構成される部分集合をAntichainと呼ぶ
Height and width
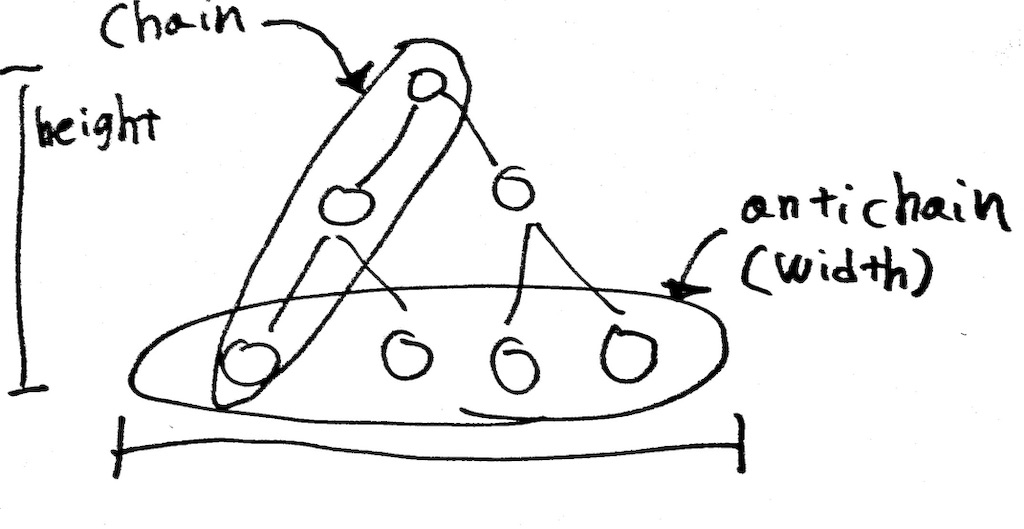
- maximal antichain:他のantichainの部分集合にならないようなantichain
- maximum antichain:poset*1の中でもっとも多くの元を含むantichain
- width:posetのmaximum antichainの濃度のこと
- posetがk個のchainに分割できる場合、antichainのwidthはk以下になります。
height:posetのchainのもつ、最大の濃度のこと
任意のantichainがchain共通部分を持つ場合、共通部分の濃度は高々1つです。
- antichainにはcomparableな元を含めないため,あるchain(任意の元のペアがcomparableな性質をもつ)の元が複数入っていることはおかしい
Sperner families
- あんまり関係なさそうなわりにハイコンテキストなので訳さない。原文↓
An antichain in the inclusion ordering of subsets of an n-element set is known as a Sperner family. The number of different Sperner families is counted by the Dedekind numbers, the first few of which numbers are
Join and meet operations
- note:ここから下はあまり自信がありません...
おそらくorder theoryにおけるJoin,meetと言う概念の理解が必要と思われる。
全てのantichainには対応する下方集合(lower set)が存在している。
ちなみに,Xの部分集合である下方集合Lは次のように定義できます*4
∀x∈L ∀y∈X: y≤x ⇨ y∈L
note:これはposetをグラフ化したとき、antichainとなる集合には必ずin-degreeが1以上にの元がある、ということかな。(antichainから開始するグラフは作れない=必ず下方集合が存在する)
対応する下方集合の違うantichain A,Bに対して以下の条件JOIN
∨操作を行うことができる。- A∨B = {x ∈ A ∪ B | !∃ y ∈ A ∪ B s.t.x<y}
似たようにmeet
∧操作を行うことができる- A∧B={x∈LA∩L|!∃y∈LA∩LB s.t. x < y}